HMM

定义

隐马儿可夫模型（hidden Markov model,HMM）是描述隐藏的马尔科夫链随机生成观测序列问题，属于生成模型。

HMM描述了一个隐藏马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生的观测随机序列的过程：

1. 隐藏马尔科夫链随机生成的状态随机序列，称为状态序列
2. 每个状态生成一个观测，由此产生的观测的随机序列，称为观测序列
3. 序列的每个位置可以看做一个时刻

HMM由初始概率分布、状态转移概率分布以及观测关于分布构成，定义如下：
$$ Q = \{q_1,q_2,…,q_n \} , V = \{v_1,v_2,…,v_m\}$$

其中$Q$可能是所有可能状态的集合，长度为$N$；$V$是所有可能观测的集合,长度为$M$

$I$对长度为$T$的状态序列，则$O$为对应的观测序列:
$$ I = (i_1,i_2,…,i_T) , O = (o_1,o_2,…,o_T)$$

• $A$是状态转移概率矩阵：$$ A = [a_{i,j}]_{N \times N}$$ 其中$ a_{i,j} = P{i_{t+1} = q_j | i_{t} = q_i}$,表示$t$时刻下为状态$q_i$转移到$t+1$时刻$q_j$状态的概率

• $B$是观测概率矩阵：$$B = [b_j(k)]_{M \times M}$$ 其中$b_j(k) = P(o_t = v_k | i_t = q_j )$，表示$t$时刻$q_j$状态生成观测$v_k$的概率

• $\pi$是初始状态概率向量：$$ \pi = (\pi_i)$$ 其中$\pi_i = P(i_t = q_i)$，表示$t=1$时状态$q_i$的概率

因此HMM由$A$、$B$和$\pi$构成（这三个矩阵/向量称为HMM三要素），同时$\pi$和$A$决定$B$，而$B$决定观测概率，即$$ \lambda = (A,B,\pi) $$

两个基本假设

从定义可知，HMM模型有两个基本假设：

1. 齐次马尔科夫性假设：隐藏的马尔科夫链在任意时刻的状态只依赖于他上一时刻的状态，与其他时刻的状态以及观测无关，也与时刻$t$无关$$P(i_t | i_{t-1},o_{t-1},…,i_1,o_1) = P(i_t|i_{t-1})$$
2. 观测独立性假设：任意时刻的观测只依赖于他当前时刻的状态，与其他时刻状态无关 $$P(o_t | i_T,o_T,…,i_{t-1},o_{t-1},…,i_1,o_1) = P(o_t|i_t)$$

三个基本问题

HMM的三个基本问题:

1. 概率计算问题：给定模型$ \lambda = (A,B,\pi) $和观测序列$O = (o_1,o_2,…,o_T)$，计算在给定模型$\lambda$下输出观测序列$O$的概率
2. 学习问题：已经观测序列$O = (o_1,o_2,…,o_T)$,用来估计模型$ \lambda = (A,B,\pi) $的参数，使得该模型下观测序列的概率$P(O|\lambda)$最大
3. 预测问题：给定模型$ \lambda = (A,B,\pi) $和观测序列$O = (o_1,o_2,…,o_T)$，求对给定观测序列条件概率$P(I|O)$最大的状态序列$I = (i_1,i_2,…,i_T)$，即给定观测序列，求最有可能的状态序列

CRF

CRF（条件随机场）是在给定一组随机变量的条件下输出另一组随机变量的条件概率分布模型，其特点是输出的随机变量构成马尔科夫随机场

概率无向图模型

概率图模型:给定一个无向图$G=(V,E)$，节点$v \in V$表示一个随机变量$Y_v$，$Y = (Y_v)_{v \in V}$，而边$e \in E$则表示两个随机变量直接的依赖关系，则他的联合概率分布为$P(Y)$

概率图的随机变量$v$之间存在三种马尔可夫性：

1. 成对马尔可夫性:$u$和$v$是两个任意不相连的节点，对应的随机变量分别是$Y_u$和$Y_v$，而$O$为其他所有的节点以及他的随机变量组为$Y_O$,则在给定随机变量组$Y_O$的条件下$Y_u$和$Y_v$是相互独立的，即$$ P(Y_u,Y_v | Y_O) = P(Y_u | Y_O) P(Y_v | Y_O)$$
2. 局部马尔可夫性性：$v$是$G$中的任意一个节点，$W$是与$v$的所有邻居节点，而$O$为其他所有的节点，他们三个的随机变量(组)分别为$Y_v,Y_W,Y_O$,则在给定随机变量组$Y_W$的条件下$Y_v$与$Y_O$是相互独立的，即$$P(Y_v,Y_O | Y_W) = P(Y_v | Y_W) P(Y_O | Y_W)$$
3. 全局马尔可夫性：节点集合$A$和$B$在无向图$G$中被节点集合$C$完美隔离开了,而$A,B,C$三组即可对应的随机变量组分别为$Y_A,Y_B,Y_C$,则在给定随机变量组$Y_C$的条件下$Y_A$和$Y_B$时候相互独立的,即$$ P(Y_A,Y_B |Y_C) = P(Y_A | Y_C) P(Y_B | Y_C) $$

注意，上述成对的、局部的和全局的马尔可夫性定义是等价的

概率无向图模型定义：在概率图模型的基础上，满足成对的、局部的或全局的马尔可夫性时，其联合概率分布$P(Y)$则称之为概率无向图模型或者是马尔科夫随机场

同时概率无向图模型的联合概率分布可以表示为其最大团$C$上随机变量函数的乘积形式操作.即$$P(Y) = \frac{1}{Z} \prod_c \psi_c(Y_c)$$

线性链条件随机场

当无向图为线性链表示的时候，该无向图$G$为：$$G = (V = \{1,2,…n\},E = \{(i,i+1)\})$$

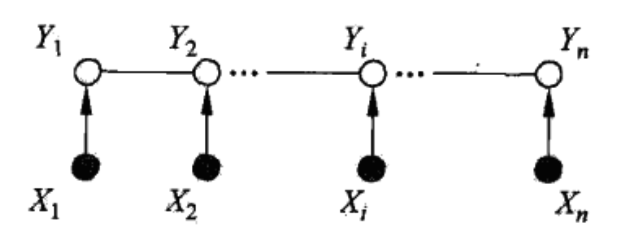
设$X=(X_1,X_2,..,X_n)$，$Y=(Y_1,Y_2,…,Y_n)$线性连表示的随机序列，若给定随机变量序列$X$的条件下，随机序列$Y$的条件概率分布构成条件随机场，则称$P(Y|X)$为线性条件随机场

在标注问题中，$X$为输入的观测序列，$Y$表示输出的标记序列或者状态序列

线性条件随机场具有如下的参数形式:
$$P(y|x) = \frac{1}{Z(x)} exp (\sum_{i,k} \lambda_k t_k (y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l (y_i,x,i) )$$ 其中
$$Z(x) = \sum_y exp (\sum_{i,k} \lambda_k t_k (y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l (y_i,x,i) )$$

1. $t_k$为定义在边上的特征函数，称为转移特征，主要依赖当前和前一个位置
2. $s_l$为定义在节点上的特征函数，称为状态特征，依赖与当前位置
3. 这两特征函数一般取值为0或者1

同时将转移特征和状态特征按位置进行合并之后，其式子可以改为简化特征：
$$P(y|x) = \frac{exp(w \cdot F(y,x))}{Z_w(x)}$$

另外如果改写为矩阵形式，给序列引入额外的起始和终点的标记状态$y_0 = \text{start},y_{n+1} = \text{stop}$,则针对每个位置$i$都可以定义一个$M$阶矩阵:$$M_i(x) = \text{exp}(\sum_i^k w_kf_k(y_{i-1},y_i,x,i))$$
$y$的非规范化概率为可以写成$n+1$个矩阵的相乘形式 $\prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)$，于是，最终的条件概率为$$P_w(y|x) = \frac{1}{Z_w(x)} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)$$

三个基本问题

CRF的三个基本问题为:

1. 概率计算问题：给定条件随机场$P(Y|X)$,输入序列是$x$和输出序列$y$，计算条件概率$P(Y_i=y_i|x)$，$P(Y_{i-1}=y_{i-1},Y_i=y_i|x)$以及相应的数据期望问题
2. 学习问题：已知经验概率分布，来计算条件随机场的模型参数
3. 预测问题：给定条件随机场$P(Y|X)$和输入序列$x$，求条件概率最大的输出序列$y$，其实就是序列标注问题

针对预测问题，其实就是求非规范化概率最大的最优路问题：$$\underset{y}{max}(w \cdot F(y,x))$$

其中$F(y,x) = \{F_i(y_{i-1},y_i,x)\}$为局部特征向量

一般使用动态规划的维特比算法来求解

1. 初始化:$$\delta_1 (j) = w \cdot F_1 (y_0=\text{start},y_1=j,x), j = 1,2,…m$$
2. 递推:对于$i=2,3,..n$
   $$\delta_i (l) =\underset{j \in 1,..m}{max} \{ \delta_{i-1}(j) + w \cdot F_i(y_{i-1}(j),y_i(l),x)\},l = 1,…m \\ \varphi_i (l) = \underset{j \in 1,..m}{max} \{ \delta_{i-1}(j) + w \cdot F_i(y_{i-1}(j),y_i(l),x) \},l = 1,…m $$
3. 终止 $$\underset{y}{max}(w \cdot F(y,x)) = \underset{j \in 1,..m}{max} \delta_n(j) \\ y^* = \underset{j \in 1,..m}{argmax} \delta_n(j)$$
4. 返回路径 $$y^* = \varphi_{i+1} (y_{i+1}^*), i = n-1,n-2,…1$$

最终维特比算法的最终复杂度为:$O(nm^2)$

BILSTM-CRF

上面提到的特征其实是模块特征，CRF模型的效果非常依赖于提取特征的模板，而通过BILSTM则可以借助神经网络自动的提取上下文的特征

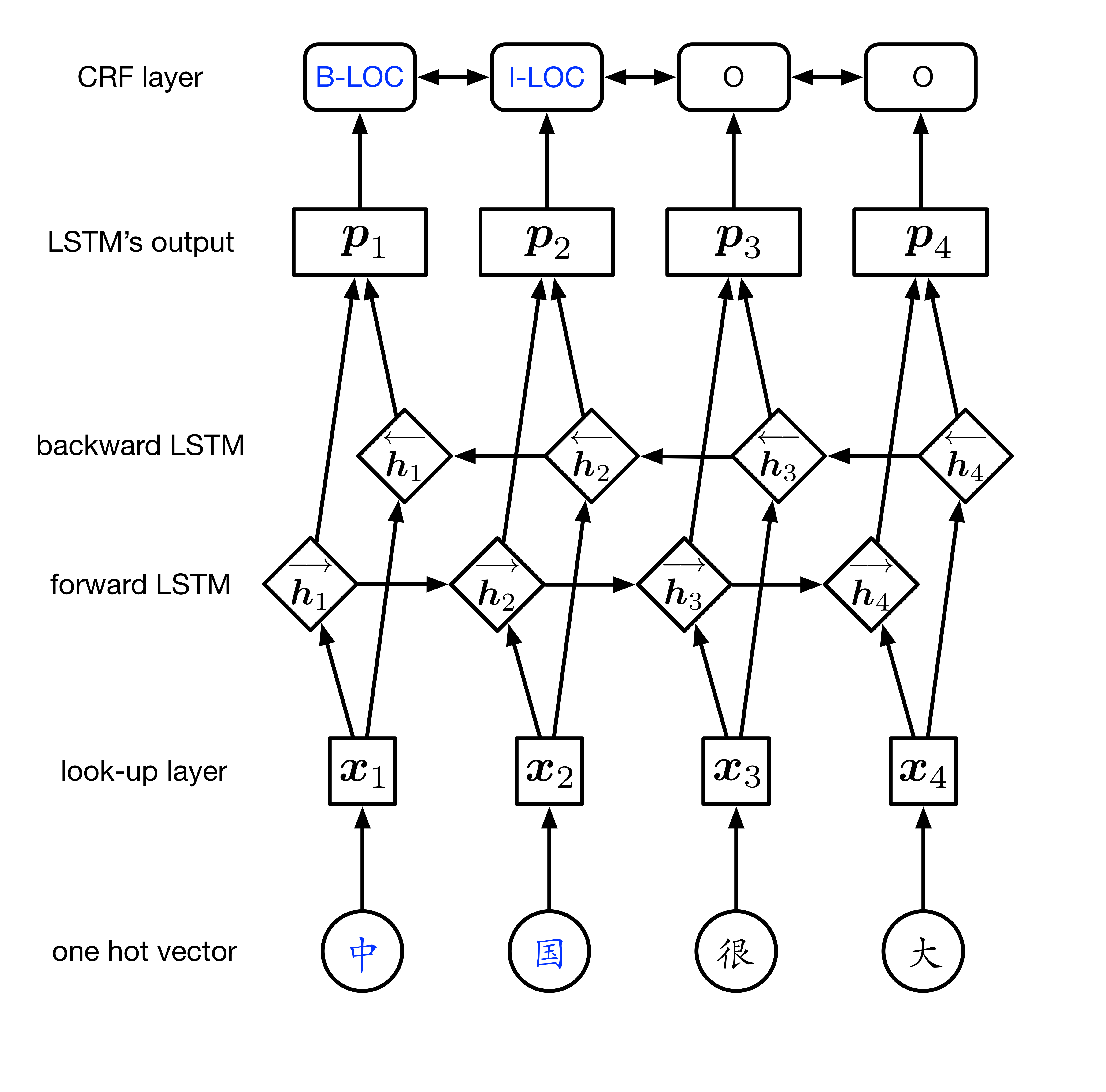
则最终的打分为:$$score(x,y) = \sum_{i=1}^n P_{i,y_i} + \sum_{i=1}^n A(y_{i-1},y_i)$$

这里：

1. $P_{i,y_i} $表示当前输入词在各个输出tag位置的分数，一般是bilstm之后过一层softmax得到，注意这里的分数已经含有整句话的上下文信息了
2. $A(y_{i-1},y_i)$是表示标签$y_{i-1}$转移到$y_i$的概率

HMM与CRF的差异

1. HMM是生成式模型，CRF是判别式模型
2. HMM是有向图，CRF是无向图
3. HMM有独立性假设，容易陷入局部最优，而CRF考虑了全局特征函数，可以全局最优解
4. HMM是先生成不可观测状态概率，再生成观测概率，而CRF是根据观测结果来生成状态概率

参考

1. 《统计学习方法》.第10、11章
2. https://guillaumegenthial.github.io/sequence-tagging-with-tensorflow.html